誤差関数や逆誤差関数に対して近似する
概要
誤差関数\(erf\)とは以下の式で定義される関数である。
\( \quad \displaystyle erf(z) = \frac{2}{\sqrt{\pi}} \displaystyle \int_0^z exp(-t^2) dt \)
この誤差関数とその逆関数である逆誤差関数を近似するのがこの研究の目標。
手順は以下のようになる。
1.boostを用い、正確な誤差関数・逆誤差関数の値を得る
2.近似手法の調査
3.多項式フィッティングを行う
boostを用い、正確な誤差関数・逆誤差関数の値を得る
近似する上で正確な誤差関数・逆誤差関数の関数値が必要になる。doubleでは有効桁数が15桁しかなく、正確な値を求めることは出来ない。
そこでboostのmultiprecisionクラスを用い、最低でも有効桁数が120桁になるよう仮数部を512bitとし計算を行った。
誤差関数の数表はこちら
逆誤差関数の数表はこちら
boostのmultiprecisionクラスを.NETで使う方法はこちら
近似手法の調査
近似式はグラフの概形と合わせる必要がある。
誤差関数近似式の条件は以下になる。
・単調増加
・\(\quad erf(0) = 0 , \quad \displaystyle \lim_{z \to \infty} erf(z) = 1 , \quad \displaystyle \lim_{z \to -\infty} erf(z) = -1 \)
誤差関数近似式の候補は以下になる。
・オイラー展開
\( \quad \displaystyle erf(z) = \frac{2}{\sqrt{\pi}} \displaystyle \sum_{n=0}^{\infty} \frac{(-1)^n z^{2n+1}}{n! (2n+1)} =\frac{2}{\sqrt{\pi}}z(1 - \frac{z^2}{3} + \frac{z^4}{10} - \frac{z^6}{42} + \frac{z^8}{216} - \ldots) \)
→× \(z\)の絶対値が大きいとき発散する
・漸近展開
\( \quad \displaystyle erf(z) = \frac{ \displaystyle \frac{2}{\sqrt{\pi}} \displaystyle \sum_{n=0}^{\infty} \frac{2^n z^{2n+1}}{(2n+1)!!} }{exp(z^2)} = \frac {\frac{2}{\sqrt{\pi}}z(1 + \frac{ 2 }{3} z^2 + \frac{4}{15} z^4 + \frac{8}{105}z^6 + \frac{16}{945} z^8 + \ldots)}{exp(z^2)} \)
→× \(z\)の絶対値が大きいとき\(exp(z^2)\)が支配的になり0に収束する
・Burmann系列[1]
\( \quad \displaystyle erf(z) = sgn(z) \sqrt{1 - exp(-z^2)} \left( 1 + \frac{2}{\sqrt{\pi}} \displaystyle \sum_{k=1}^{\infty} c_k \left( exp(-z^2) \right)^k \right) \)
→○ \(z\)の絶対値が大きいとき\(exp(-z^2)\)が無視できるようになり\(\pm 1\)に収束する
逆誤差関数近似式の条件は以下になる。
・単調増加
・\( \quad \displaystyle erf^{-1}(0) = 0 , \quad \displaystyle \lim_{z \to 1^{-}} erf^{-1}(z) = \infty , \quad \displaystyle \lim_{z \to -1^{+}} erf^{-1}(z) = -\infty \)
誤差関数近似式は以下を用いる。
・Winitzki の近似 (2008)[2]
\( \quad erf^{-1}(z) \approx sgn(z) \sqrt{ \sqrt{ \left( \frac{2}{\pi a} + \frac{log(1-z^2)}{2} \right)^2 -\frac{log(1-z^2)}{a} } - \left( \frac{2}{\pi a} + \frac{log(1-z^2)}{2} \right)} \)
→○ \(z\)が\(\pm 1\)に近いとき\(\pm \infty\)に発散する
今回は\(a\)を\(z\)に応じて値を変えることでより逆誤差関数に近づける。
多項式フィッティングを行う
逆誤差関数の近似式の係数\(\frac{2}{\sqrt{pi}} c_k \)、逆誤差関数の\(a\)を\(z\)の多項式として多項式フィッティングを行った。
多項式フィッティングについてはこちら
ソースコード
namespace ExRandom {
public static class ErrorFuntion {
public static double Erf(double z) {
const double r1 = 2.6014107997561636e-1, r2 = -8.6953813580559158e-1, r3 = 4.3847519341361751e-0, r4 = -1.4284260737632032e+1,
r5 = 2.7811799647198164e+1, r6 = -3.1384758147666584e+1, r7 = 1.8906402868436025e+1, r8 = -4.6968270563253212e+0;
double w = Math.Exp(-z * z);
return Math.Sign(z) * Math.Sqrt(1 - w) * (1 + w * (r1 + w * (r2 + w * (r3 + w * (r4 + w * (r5 + w * (r6 + w * (r7 + w * r8))))))));
}
public static double InverseErf(double z) {
const double a0 = 8 * (Math.PI - 3) / (3 * Math.PI * (4 - Math.PI));
const double r1 = 5.6132012925262991e-3, r2 = 2.7658193450059033e-3, r3 = 2.9671386394640453e-3, r4 = 1.7565890613956969e-3,
r5 = 1.6739456617098636e-3, r6 = 8.2662381153020270e-4, r7 = 7.3051868901041761e-4, r8 = 2.9691095058959061e-4,
limit_scale = 500, limit_thr = 1 - 1 / limit_scale, rl1 = 5.1198322059703080e-4, rl2 = 2.1652066531156113e-3;
double z2 = z * z, z4 = z2 * z2, z8 = z4 * z4, z16 = z8 * z8, z32 = z16 * z16, z64 = z32 * z32, z128 = z64 * z64, z256 = z128 * z128;
double a = a0 + r1 * z2 + r2 * z4 + r3 * z8 + r4 * z16 + r5 * z32 + r6 * z64 + r7 * z128 + r8 * z256;
if(Math.Abs(z) > limit_thr) {
double z_limit = (Math.Abs(z) - limit_thr) * limit_scale;
a -= rl1 * Math.Pow(z_limit, 4) + rl2 * Math.Pow(z_limit, 32);
}
double w = Math.Log(1 - z2), u = 2 / (Math.PI * a) + w / 2;
return Math.Sign(z) * Math.Sqrt(Math.Sqrt(u * u - w / a) - u);
}
public static double NormalCDF(double s) {
return (Erf(s / Math.Sqrt(2)) + 1) / 2;
}
public static double Probit(double p) {
return Math.Sqrt(2) * InverseErf(2.0 * p - 1.0);
}
}
}
評価
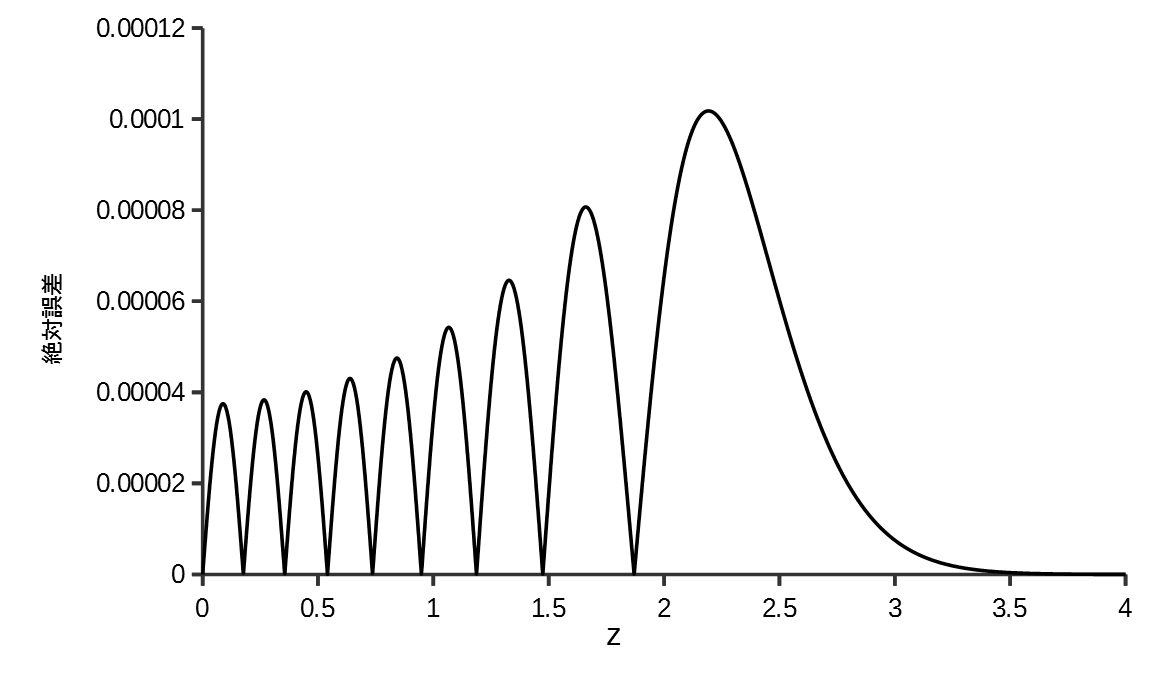
誤差関数の近似最大誤差は\(z=\pm 2.19\)のとき\(1.018 \times 10^{-4}\)となり、文献[1]の式(33)pp29の近似式の最大誤差\(3.613 \times 10^{-3}\)より小さくなる。
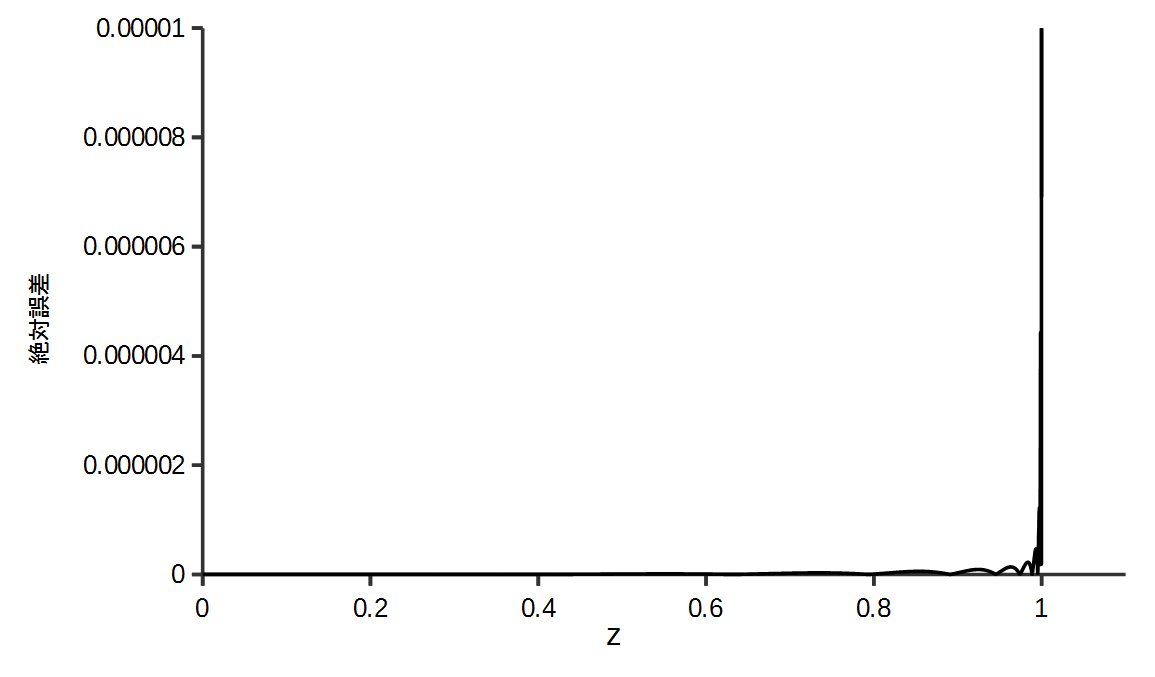
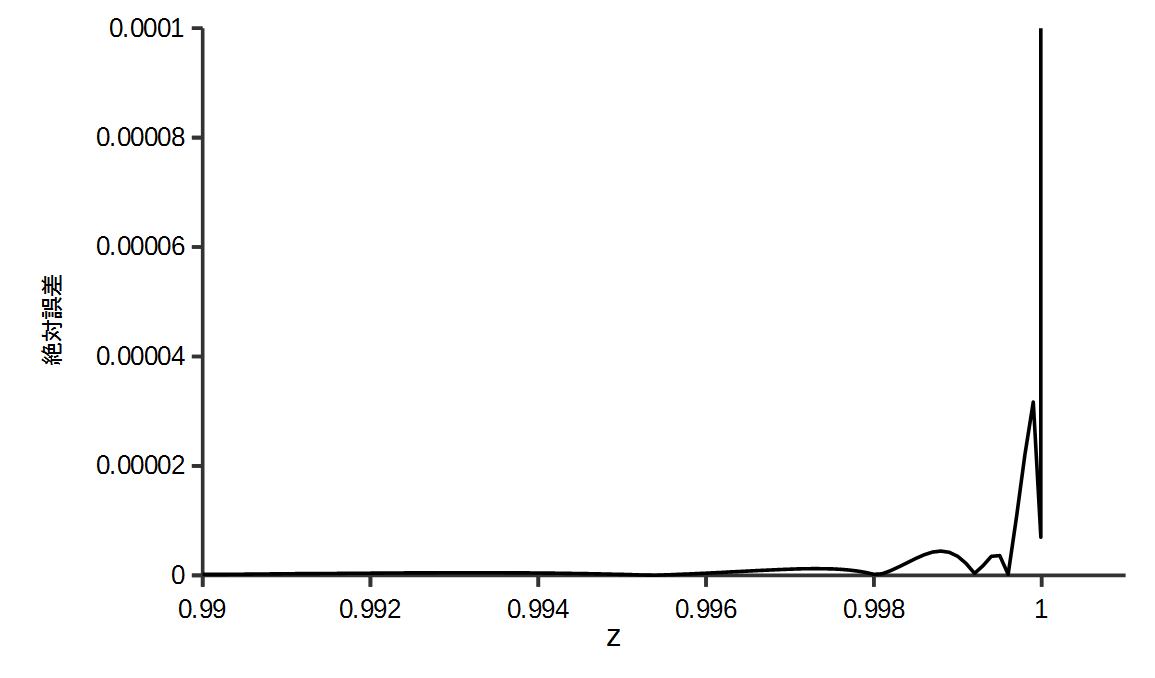
逆誤差関数の近似誤差は\(z=\pm 0.999\)のとき\(3.462 \times 10^{-6}\)となり、文献[2]の近似式の誤差\(3.5 \times 10^{-3}\)より小さくなる。
最大誤差は\(z=\pm 1\)で\(\pm \infty\)に発散する逆誤差関数の性質上得ることができない。
さらに精度を上げる
誤差関数\(erf\)の精度をさらに上げたい。近似式について考える。
\( \quad \displaystyle erf(z) = sgn(z) \sqrt{1 - exp(-z^2)} \left( 1 + \frac{2}{\sqrt{\pi}} \displaystyle \sum_{k=1}^{\infty} c_k \left( exp(-z^2) \right)^k \right) \)
多項式を用いて近似した部分を\(g(w), \ w = exp(-z^2), \ r_k = \frac{2}{\sqrt{\pi}} c_k \)とする。
\( \quad g(w) = \displaystyle \sum_{k=1}^{\infty} r_k w \)
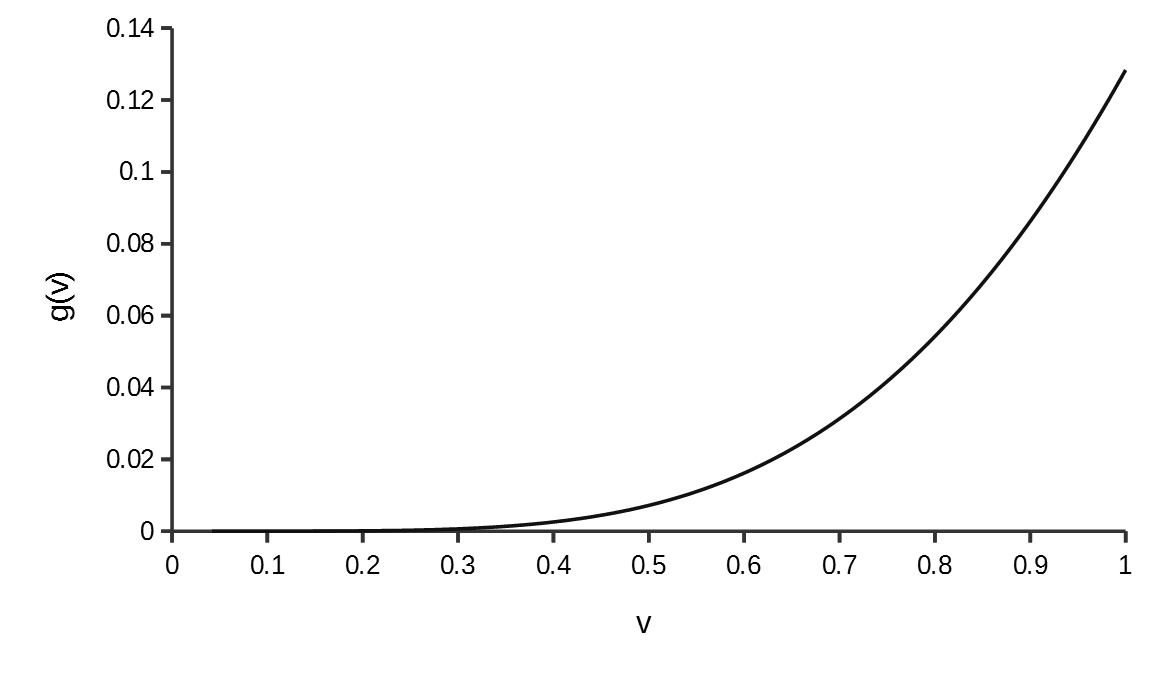
このとき\(g(w), 0 \lt w \leq 1\)は以下のようになる。
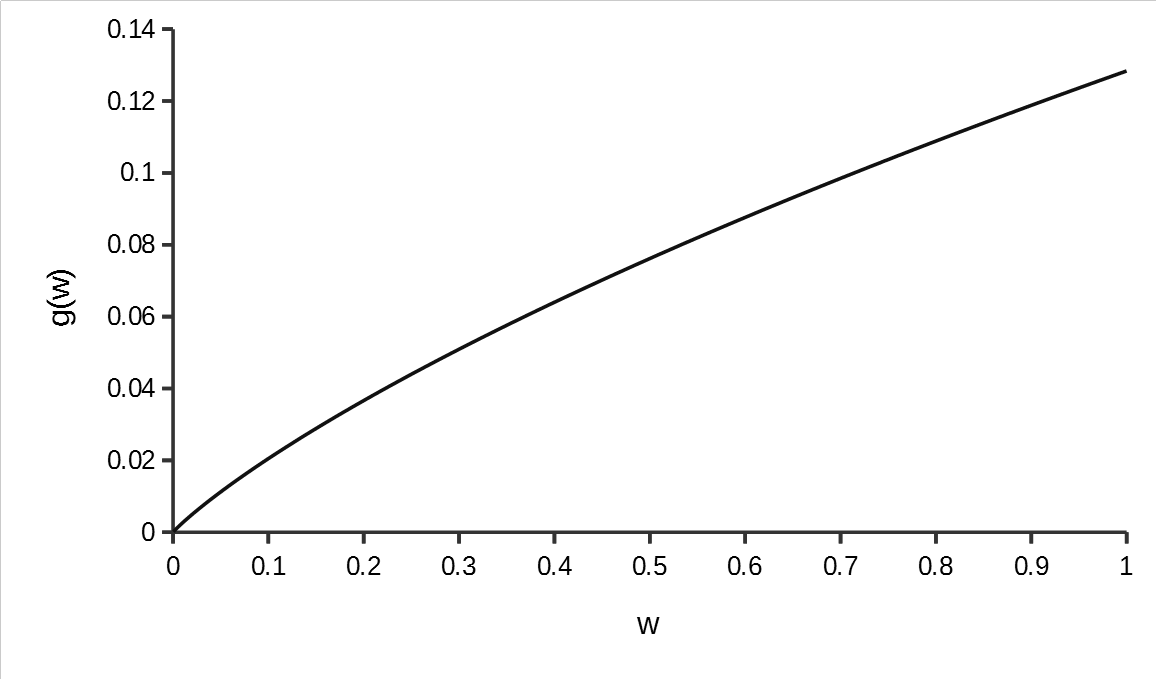
この\(0\)近傍よりも\(0\)より遠い領域の方が傾きが小さくなるような関数は、多項式の次数を上げたとしてもその収束速度が遅い。(ルンゲ現象が生じるため。)
こういう場合は独立変数\(v\)を変数変換して多項式近似しやすい関数に変換してやれば良い。\(v = w^p, \ p = 0.19825\)
\( \quad g(v) = \displaystyle \sum_{k=1}^{\infty} {r'}_k v \)
この変数変換を用いて算出したより近似精度の高い近似式は以下のようになる。
\( \quad \displaystyle erf(z) = sgn(z) \sqrt{1 - exp(-z^2)} \left( 1 + \displaystyle \sum_{k=1}^{20} r_k \left( exp(-z^2) \right) ^{p k} \right) \)
\( \begin{eqnarray} \quad p \ &=& \ \ \ 1.6512015193530959799357169 &\times& 10^{-1} \\ \quad r_{1} &=& -1.5315272736367919136465908 &\times& 10^{-11} \\ \quad r_{2} &=& +3.9615730720676436116503029 &\times& 10^{-9} \\ \quad r_{3} &=& -3.5976507445494357229780264 &\times& 10^{-7} \\ \quad r_{4} &=& +1.8049568114837651503748071 &\times& 10^{-5} \\ \quad r_{5} &=& -7.3030246172865295988921901 &\times& 10^{-4} \\ \quad r_{6} &=& +3.2914553426705589009037522 &\times& 10^{-1} \\ \quad r_{7} &=& -1.1694151047539977156039503 &\times& 10^{-1} \\ \quad r_{8} &=& -5.1672892101940304697375886 &\times& 10^{-2} \\ \quad r_{9} &=& -3.4922038136944812893880727 &\times& 10^{-1} \\ \quad r_{10} &=& +1.7848481461777636291754195 &\times& 10^{0} \\ \quad r_{11} &=& -7.1779133907214715535310867 &\times& 10^{0} \\ \quad r_{12} &=& +2.0251989430600462686777455 &\times& 10^{1} \\ \quad r_{13} &=& -4.1667927478555565145940204 &\times& 10^{1} \\ \quad r_{14} &=& +6.4771543719245865936433467 &\times& 10^{1} \\ \quad r_{15} &=& -7.5078011565202963371960207 &\times& 10^{1} \\ \quad r_{16} &=& +6.2984565504151589666979890 &\times& 10^{1} \\ \quad r_{17} &=& -3.6882757962765197822157621 &\times& 10^{1} \\ \quad r_{18} &=& +1.4274796989932290111206046 &\times& 10^{1} \\ \quad r_{19} &=& -3.2839882315464206366446257 &\times& 10^{0} \\ \quad r_{20} &=& +3.4063586417140949890821044 &\times& 10^{-1} \end{eqnarray} \)
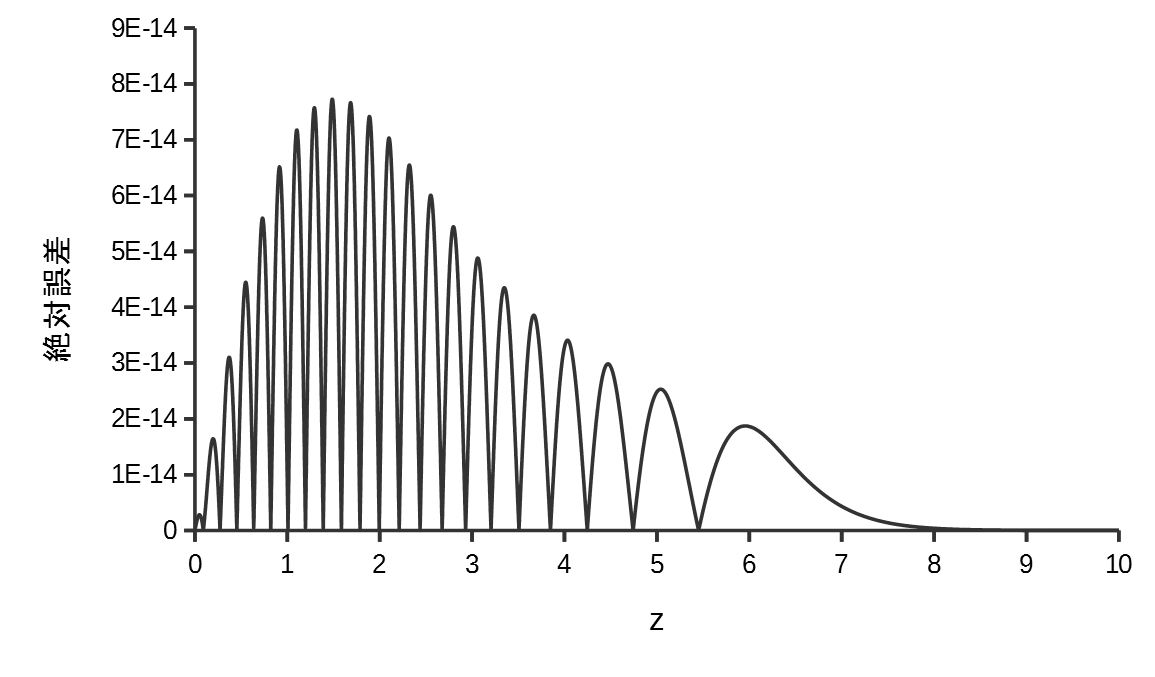
近似した結果が以下になる。最大誤差は\(z = \pm 1.485\)のとき\(7.730 \times 10^{-14}\)となった。
これ以上次数を上げるとdoubleの丸め誤差でかえって誤差が増えてしまう。
namespace ExRandom {
public static class ErrorFuntion {
static double Erf(double z) {
const double p = 1.6512015193530959799357169e-01;
const double r1 = -1.5315272736367919136465908e-11;
const double r2 = +3.9615730720676436116503029e-09;
const double r3 = -3.5976507445494357229780264e-07;
const double r4 = +1.8049568114837651503748071e-05;
const double r5 = -7.3030246172865295988921901e-04;
const double r6 = +3.2914553426705589009037522e-01;
const double r7 = -1.1694151047539977156039503e-01;
const double r8 = -5.1672892101940304697375886e-02;
const double r9 = -3.4922038136944812893880727e-01;
const double r10 = +1.7848481461777636291754195e+00;
const double r11 = -7.1779133907214715535310867e+00;
const double r12 = +2.0251989430600462686777455e+01;
const double r13 = -4.1667927478555565145940204e+01;
const double r14 = +6.4771543719245865936433467e+01;
const double r15 = -7.5078011565202963371960207e+01;
const double r16 = +6.2984565504151589666979890e+01;
const double r17 = -3.6882757962765197822157621e+01;
const double r18 = +1.4274796989932290111206046e+01;
const double r19 = -3.2839882315464206366446257e+00;
const double r20 = +3.4063586417140949890821044e-01;
double w = Math.Exp(-z * z), v = Math.Pow(w, p);
return Math.Sign(z) * Math.Sqrt(1 - w) *
(1 + v * (r1 + v * (r2 + v * (r3 + v * (r4 + v * (r5 + v * (r6 + v * (r7 + v * (r8 + v * (r9 + v * (r10 +
v * (r11 + v * (r12 + v * (r13 + v * (r14 + v * (r15 + v * (r16 + v * (r17 + v * (r18 + v * (r19 + v * r20))))))))))))))))))));
}
}
}
引用文献
[1] “On Burmann's Theorem and Its Application to Problems of Linear and Nonlinear Heat Transfer and Diffusion", H.M.Schopf, P.H.Supancic, The Mathematica Journal, vol.16, 2014
[2] “A Handy approximation for the error functon and its inverse", Sergei Winitzki, February, 2008
