サポートベクタマシン理論編 - わかばテクノロジ

クラスタリング
サポートベクタマシン理論編; Theory of Support Vector Machine

概要

この記事ではサポートベクタマシン[1]とは何か、また実装する上で必要な理論について述べる。
サポートベクタマシンの実装についてはこちら

サポートベクタマシンは多次元ベクトルで表現された2クラスに属するデータ集合のパターンを学習し、未知のデータに対しどちらのクラスに属するか識別するクラスタリング手法の一つである。
サポートベクタマシンの目的は2クラスに属するデータ集合を分離する、マージンが最大となる分離超平面を得ることである。

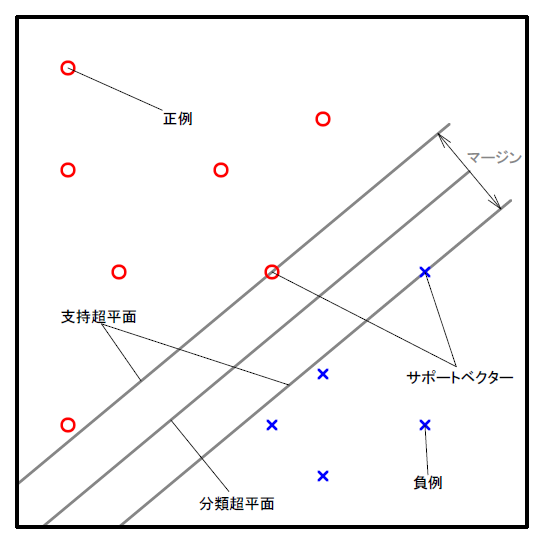
定式化

サポートベクタマシンの定式表現は以下のようになる。
データ : $ \boldsymbol{s} = (\boldsymbol{x}, y) $
データ集合 : $ \boldsymbol{S} = {\{\boldsymbol{s_i}\}}_{i=1}^{N} $
データベクトル : $ \boldsymbol{x} \in \mathbb{R}^p $
データクラス : $ y \in \{ -1, +1 \}$
線形識別関数 : $ \tilde{y} = sign( \boldsymbol{\tilde{x}} \cdot \boldsymbol{w} - h ) $
ベクトル重み : $ \boldsymbol{w} $
しきい値 : $ h $
符号関数 : $sign(r)=\begin{cases} -1 & \quad r < 0 \\ 0 & \quad r = 0 \\ +1 & \quad r > 0 \end{cases} $
識別ベクトル : $ \tilde{\boldsymbol{x}} $
識別値 : $ \tilde{y} $
分類超平面 : $ \{ \boldsymbol{x} \in \mathbb{R}^p | \boldsymbol{x} \cdot \boldsymbol{w} - h = 0 \} $
支持超平面 : $ \{ \boldsymbol{x} \in \mathbb{R}^p | \boldsymbol{x} \cdot \boldsymbol{w} - h = \pm 1 \} $
マージン : $d = 2 / | \boldsymbol{w} |$
サポートベクター : $ \boldsymbol{S_s} = \{ \boldsymbol{s_j} | \boldsymbol{s_j} \in \boldsymbol{S}, y_j (\boldsymbol{x_j} \cdot \boldsymbol{w} - h) = 1 \}_{j=1}^{V} $

としたとき、サポートベクターマシンの課題は以下のようになる。
目的関数 : マージンを最大化する $$ minimize. \quad L(\boldsymbol{w}) = \frac{1}{2} |\boldsymbol{w}|^2 $$ 制約条件 : すべてのデータについて支持超平面で分離している $$ subject \ to. \quad y_i (\boldsymbol{x_i} \cdot \boldsymbol{w} - h) \geq 1 \quad (i = 1 \dots N) $$ 最適化の対象となるパラメータ $$ {\boldsymbol{w}}^{*}, h^{*} = \displaystyle \min_{\boldsymbol{w}, h} L(\boldsymbol{w}) $$
この二次計画問題を解くためにラグランジュ緩和を用いる。

ラグランジュ未定乗数法

ラグランジュ未定乗数法とは制約条件のもとで最適化を行うための手法の一つである。各制約条件に対して未定乗数を用意し、それらを係数とする線形結合を新しい関数とすることで制約条件を一般の極値問題として解くことができる。

制約条件$g_i(\boldsymbol{w}) = 0 \ (i = 1 \cdots N) $のもとで目的関数$f(\boldsymbol{w})$が${\boldsymbol{w}}^{*} $で極値を持つとする。
ラグランジュ未定乗数を$\lambda_i \ (i = 1 \cdots N) $としてラグランジュ関数$F$を定義する。 $$ F(\boldsymbol{w}, \boldsymbol{\lambda}) = f(\boldsymbol{w}) + \displaystyle \sum_{i=1}^{N} \lambda_i g_i(\boldsymbol{w}), \quad \lambda_i \neq 0 $$ ${\boldsymbol{w}}^{*} $において以下が成り立つ $$ \frac{ \partial F }{ \partial \boldsymbol{w} } = 0, \quad \frac{ \partial F }{ \partial \boldsymbol{\lambda} } = 0 $$ 目的関数と制約問題が全て線形性となる線形計画問題(linear programming problem, LP)ではこの手法を用いて簡単に解くことができるが非線形計画問題(nonlinear programming problem, NLP)は極値となる点が局所解か最適解かどうか判定する必要がある。

[例題]
$ maximaize. \quad f(x, y) = x y $
$subject \ to. \quad 2(x + y) = 1 $

$ g(x, y)=2(x+y)-1 = 0 $
$ F(x, y, \lambda) = f(x, y) + \lambda g(x, y) = xy + 2 x \lambda + 2 y \lambda - \lambda $
$ \begin{eqnarray} \frac{ \partial F }{ \partial x } &=& y + 2 \lambda = 0 \\ \frac{ \partial F }{ \partial y } &=& x + 2 \lambda = 0 \\ \frac{ \partial F }{ \partial \lambda } &=& 2 x + 2 y - 1 = 0 \end{eqnarray} $
$\rightarrow x=y = 1/4, \lambda = -1/8 \quad f(x, y)=1/16 \ [max]　$

カルーシュ・キューン・タッカー条件(KKT条件)

制約条件が不等号を含む場合を考える
$ maximaize. \quad f(\boldsymbol{w}) $
$subject \ to. \quad g_i(\boldsymbol{w}) = 0 , \ h_j(\boldsymbol{w}) \leq 0 \quad (i = 1 \dots M,\ j = 1 \dots N) $

この問題に対応するラグランジュ関数は以下になる
$ F(\boldsymbol{w}, \boldsymbol{\alpha}, \boldsymbol{\beta}) = f(\boldsymbol{w}) + \displaystyle \sum_{i=1}^{M} \alpha_i g_i(\boldsymbol{w}) + \displaystyle \sum_{i=1}^{N} \beta_j h_j(\boldsymbol{w}), \quad (\alpha_i \neq 0, \ \beta_j \geq 0) $
なお、$f(\boldsymbol{w})$について最大化するときは$\boldsymbol{\beta}$の項の符号を負にする。

この問題にはカルーシュ・キューン・タッカー条件(KKT条件)を用いる。(厳密には正規条件を満たしているか検証する必要がある。)
最適化問題の解が存在する必要十分条件は、最適解${\boldsymbol{w}}^{*}$において次の3条件が成り立つような$\boldsymbol{\alpha}, \boldsymbol{\beta}$が存在することである。 $$ \frac{ \partial F }{ \partial \boldsymbol{w} } = 0, \quad \frac{ \partial F }{ \partial \boldsymbol{\alpha} } = 0, \quad \beta_j h_j({\boldsymbol{w}}^{*})=0 \ (j = 1 \cdots N) $$

[例題]
$minimize. \quad f(x, y, z) = -xyz $
$subject \ to. \quad x \geq 0, y \geq 0, z \geq 1, x+y+z=2 $

$ g(x, y, z)=x+y+z-2=0, \ h_1(x, y, z)=-x \leq 0, \ h_2(x, y, z)=-y \leq 0, \ h_3(x, y, z)=1-z \leq 0 $
$F(x, y, z, \alpha, \beta_1, \beta_2, \beta_3) = -xyz + \alpha (x+y+z-2)-\beta_1 x - \beta_2 y + \beta_3 (1 - z) $
$ \begin{eqnarray} \frac{ \partial F }{ \partial x } &=& -yz+\alpha-\beta_1 = 0 \\ \frac{ \partial F }{ \partial y } &=& -xz+\alpha-\beta_2 = 0 \\ \frac{ \partial F }{ \partial z } &=& -xy+\alpha-\beta_3 = 0 \end{eqnarray} $
$ \beta_1 h_1(x, y, z) = - \beta_1 x = 0, \ \beta_2 h_2(x, y, z) = -\beta_2 y = 0, \ \beta_3 h_3(x, y, z)=\beta_3 (1-z) = 0 $
$if[x=0] \quad f(x, y, z)=0 $
$if[y=0] \quad f(x, y, z)=0 $
$if[x \neq 0, y \neq 0, \beta_3 = 0] \quad x=y=z=2/3 \cdots (\times z\geq 1) $
$if[x \neq 0, y \neq 0, \beta_3 \neq 0] \quad x=y=1/2,\ z=1 \quad f(x, y, z)=-1/4 \ [min] $

ラグランジュ緩和

ラグランジュ緩和とはラグランジュ未定乗数法を用い、制約条件の一部を目的関数の中にペナルティ項として組み込み変形させる手法である。
問題Pが以下に与えられているとき
$minimize. \quad f(\boldsymbol{w}) $
$subject \ to. \quad g(\boldsymbol{w})=0 $

Pのラグランジュ緩和は以下となる
$minimize. \quad f(\boldsymbol{w}) + \lambda g(\boldsymbol{w}) $
$subject \ to. \quad \lambda \neq 0 $

SVMのパラメータ最適化

サポートベクターマシンの定式からパラメータ$\boldsymbol{w}, h$の決定式を導出する。まず、目的関数と制約条件からラグランジュ関数を求める
$minimize. \quad L(\boldsymbol{w}) = \frac{1}{2} |\boldsymbol{w}|^2 $
$subject \ to. \quad y_i ( \boldsymbol{x_i} \cdot \boldsymbol{w} - h ) \geq 1 $

ラグランジュ関数およびその$\boldsymbol{w}, h $の偏微分は以下になる
$ \begin{eqnarray} F(\boldsymbol{w}, h, \boldsymbol{a}) &=&\displaystyle \frac{1}{2} |\boldsymbol{w}|^2 - \displaystyle \sum_{i=1}^{N} a_i (y_i ( \boldsymbol{x_i} \cdot \boldsymbol{w} - h ) - 1) \quad \quad a_i \geq 0 \\ &=&\displaystyle \frac{1}{2} |\boldsymbol{w}|^2 - \displaystyle \sum_{i=1}^{N} a_i y_i \boldsymbol{x_i} \cdot \boldsymbol{w} - a_i y_i h - a_i \\ &=&\displaystyle \frac{1}{2} |\boldsymbol{w}|^2 - \displaystyle \sum_{i=1}^{N} a_i y_i \boldsymbol{x_i} \cdot \boldsymbol{w} + h \sum_{i=1}^{N} a_i y_i + \sum_{i=1}^{N} a_i \\ \end{eqnarray}$
$ \displaystyle \frac{\partial F}{\partial \boldsymbol{w}} = \boldsymbol{w} - \displaystyle \sum_{i=1}^{N} a_i y_i \boldsymbol{x_i} = 0 \rightarrow \boldsymbol{w} = \sum_{i=1}^{N} a_i y_i \boldsymbol{x_i} $
$ \displaystyle \frac{\partial F}{\partial h} = \displaystyle \sum_{i=1}^{N} a_i y_i = 0 $

次に偏微分によって求められた2式をラグランジュ関数に代入し双対問題にする。
$ \begin{eqnarray} F(\boldsymbol{w}, h, \boldsymbol{a}) &=& L( \boldsymbol{a} ) \\ &=&\displaystyle \frac{1}{2} |\boldsymbol{w}|^2 - \displaystyle \sum_{i=1}^{N} a_i y_i \boldsymbol{x_i} \cdot \boldsymbol{w} + h \sum_{i=1}^{N} a_i y_i + \sum_{i=1}^{N} a_i \\ &=&\displaystyle \frac{1}{2} \displaystyle \sum_{i, j=1}^{N} a_i a_j y_i y_j \boldsymbol{x_i} \cdot \boldsymbol{x_j} - \displaystyle \sum_{i, j=1}^{N} a_i a_j y_i y_j \boldsymbol{x_i} \cdot \boldsymbol{x_j} + \sum_{i=1}^{N} a_i \\ &=&\displaystyle \sum_{i=1}^{N} a_i - \displaystyle \frac{1}{2} \displaystyle \sum_{i, j=1}^{N} a_i a_j y_i y_j \boldsymbol{x_i} \cdot \boldsymbol{x_j} \\ \end{eqnarray}$
$maximize. \quad L(\boldsymbol{a}) = \displaystyle \sum_{i=1}^{N} a_i - \displaystyle \frac{1}{2} \displaystyle \sum_{i, j=1}^{N} a_i a_j y_i y_j \boldsymbol{x_i} \cdot \boldsymbol{x_j} $
$subject \ to. \quad a_i \geq 0, \displaystyle \sum_{i=1}^{N} a_i y_i = 0 $

目的関数を最大化する$ {\boldsymbol{a}}^{*} $が求まれば以下の式で最適なパラメータ$ {\boldsymbol{w}}^{*}, {\boldsymbol{h}}^{*} $を求めることができる
なお、$\boldsymbol{S_s}, \boldsymbol{x_s}, y_s $はサポートベクターの集合、データベクトル、データクラスである
$ {\boldsymbol{w}}^{*} = \displaystyle \sum_{ (\boldsymbol{x_s}, y_s) \in \boldsymbol{S_s}} {a_i}^{*} y_s \boldsymbol{x_s}, \ h^{*} = {\boldsymbol{w}}^{*} \cdot \boldsymbol{x_s} - y_s $

ソフトマージンSVM

サポートベクターマシンは線形分離可能な場合しか用いることはできない。線形分離不可能なとき識別誤りに対するペナルティを設け拡張したものがソフトマージンSVMである。分類超平面を超えて反対側に入ってしまったサンプルのデータベクトルと分類超平面との距離をパラメータ$ \epsilon_i (\geq 0) $を用いて$ \frac{\epsilon_i}{|\boldsymbol{w}|^2} $で表す
ここで$ \displaystyle \sum_{i=1}^{N} \epsilon_i $をならべく小さくしたい
なおコストパラメータ$C$はペナルティの大きさを決める定数であり小さいほど識別誤りに対するペナルティは小さくなる

$minimize. \quad L(\boldsymbol{w}) = \displaystyle \frac{1}{2} |\boldsymbol{w}|^2 + \displaystyle C \sum_{i=1}^{N} \epsilon_i $
$subject \ to. \quad y_i \cdot ( \boldsymbol{x_i} \cdot \boldsymbol{w} - h ) \geq 1 - \epsilon_i, \ \epsilon_i \geq 0 $

ラグランジュ関数およびその$\boldsymbol{w}, h, \epsilon_i $の偏微分は以下になる
$ \begin{eqnarray} F(\boldsymbol{w}, h, \boldsymbol{a}) &=&\displaystyle \frac{1}{2} |\boldsymbol{w}|^2 + \displaystyle C \sum_{i=1}^{N} \epsilon_i - \displaystyle \sum_{i=1}^{N} a_i (y_i ( \boldsymbol{x_i} \cdot \boldsymbol{w} - h ) - (1 - \epsilon_i)) - \sum_{i=1}^{N} \mu_i \epsilon_i \quad \quad a_i \geq 0, \ \mu_i \geq 0 \\ &=&\displaystyle \frac{1}{2} |\boldsymbol{w}|^2 + \displaystyle C \sum_{i=1}^{N} \epsilon_i - \displaystyle \sum_{i=1}^{N} a_i y_i \boldsymbol{x_i} \cdot \boldsymbol{w} - a_i y_i h - a_i + a_i \epsilon_i - \sum_{i=1}^{N} \mu_i \epsilon_i \\ &=&\displaystyle \frac{1}{2} |\boldsymbol{w}|^2 + \displaystyle C \sum_{i=1}^{N} \epsilon_i - \displaystyle \sum_{i=1}^{N} a_i y_i \boldsymbol{x_i} \cdot \boldsymbol{w} + h \sum_{i=1}^{N} a_i y_i + \sum_{i=1}^{N} a_i - \sum_{i=1}^{N} a_i \epsilon_i - \sum_{i=1}^{N} \mu_i \epsilon_i \\ \end{eqnarray}$
$ \displaystyle \frac{\partial F}{\partial \boldsymbol{w}} = \boldsymbol{w} - \displaystyle \sum_{i=1}^{N} a_i y_i \boldsymbol{x_i} = 0 \rightarrow \boldsymbol{w} = \sum_{i=1}^{N} a_i y_i \boldsymbol{x_i} $
$ \displaystyle \frac{\partial F}{\partial h} = \displaystyle \sum_{i=1}^{N} a_i y_i = 0 $
$ \displaystyle \frac{\partial F}{\partial \epsilon_i} = C - a_i - \mu_i = 0 \rightarrow a_i = C - \mu_i \rightarrow a_i \leq C $

次に偏微分によって求められた3式をラグランジュ関数に代入し双対問題にする
$ \begin{eqnarray} F(\boldsymbol{w}, h, \boldsymbol{a}, \boldsymbol{\mu}) &=& L( \boldsymbol{a} ) \\ &=&\displaystyle \sum_{i=1}^{N} a_i - \displaystyle \frac{1}{2} \displaystyle \sum_{i, j=1}^{N} a_i a_j y_i y_j \boldsymbol{x_i} \cdot \boldsymbol{x_j} + C \displaystyle \sum_{i}^{N} \epsilon_i - \sum_{i}^{N} a_i \epsilon_i - \sum_{i}^{N} \mu_i \epsilon_i \\ &=&\displaystyle \sum_{i=1}^{N} a_i - \displaystyle \frac{1}{2} \displaystyle \sum_{i, j=1}^{N} a_i a_j y_i y_j \boldsymbol{x_i} \cdot \boldsymbol{x_j} + C \displaystyle \sum_{i}^{N} \epsilon_i - \sum_{i}^{N} (C - \mu_i) \epsilon_i - \sum_{i}^{N} \mu_i \epsilon_i \\ &=&\displaystyle \sum_{i=1}^{N} a_i - \displaystyle \frac{1}{2} \displaystyle \sum_{i, j=1}^{N} a_i a_j y_i y_j \boldsymbol{x_i} \cdot \boldsymbol{x_j} \\ \end{eqnarray}$
$maximize. \quad L(\boldsymbol{a}) = \displaystyle \sum_{i=1}^{N} a_i - \displaystyle \frac{1}{2} \displaystyle \sum_{i, j=1}^{N} a_i a_j y_i y_j \boldsymbol{x_i} \cdot \boldsymbol{x_j} $
$subject \ to. \quad 0 \leq a_i \leq C, \displaystyle \sum_{i=1}^{N} a_i y_i = 0 $

つまりSVMから制限条件が1つ加わった問題に帰着することが出来る

カーネルSVM

上記2つのSVMは分離面を平面とするものであったが、カーネルSVMはベクトル内積のかわりにカーネル関数を用いることで分離面を曲面にすることができる

カーネルSVMの定式化
$maximize. \quad L(\boldsymbol{a}) = \displaystyle \sum_{i=1}^{N} a_i - \displaystyle \frac{1}{2} \displaystyle \sum_{i, j=1}^{N} a_i a_j y_i y_j K(\boldsymbol{x_i}, \boldsymbol{x_j}) $
$subject \ to. \quad 0 \leq a_i \leq C, \displaystyle \sum_{i=1}^{N} a_i y_i = 0 $

最適パラメータ
$ {\boldsymbol{w}}^{*} = \displaystyle \sum_{ (\boldsymbol{x_s}, y_s) \in \boldsymbol{S_s}} {a_i}^{*} y_s \boldsymbol{x_s}, \ h^{*} = K({\boldsymbol{w}}^{*}, \boldsymbol{x_s}) - y_s $
識別関数
$ \tilde{y} = sign( \displaystyle \sum_{ (\boldsymbol{x_s}, y_s) \in \boldsymbol{S_s}} {a_i}^{*} y_s K(\boldsymbol{x_s}, \boldsymbol{ \tilde{x}}) - h^{*} )$

カーネル関数には以下の様なものがある
$p$次多項式カーネル
$K(\boldsymbol{x_1}, \boldsymbol{x_2}) = (c + \boldsymbol{x_1} \cdot \boldsymbol{x_2})^p $
ガウシアンカーネル
$K(\boldsymbol{x_1}, \boldsymbol{x_2}) = exp \left( \frac{ -|\boldsymbol{x_1} - \boldsymbol{x_2} |^2 }{2 \sigma ^ 2} \right) $

逐次最小問題最適化法

逐次最小問題最適化法[2]は二次計画問題に帰着した問題、特にSVMで用いられるアルゴリズムである
なお二次計画問題(quadratic programming problem, QP)とは目的関数が二次関数であり制約条件が一次関数である最適化問題のことである。

カーネルソフトマージンSVMにおける問題は以下の式で表現された
$maximize. \quad L(\boldsymbol{a}) = \displaystyle \sum_{i=1}^{N} a_i - \displaystyle \frac{1}{2} \displaystyle \sum_{i, j=1}^{N} a_i a_j y_i y_j K(\boldsymbol{x_i}, \boldsymbol{x_j}) $
$subject \ to. \quad 0 \leq a_i \leq C, \displaystyle \sum_{i=1}^{N} a_i y_i = 0 $

この式を2つのラグランジュ乗数$a_1, a_2 $について部分問題として見てみる
$\begin{eqnarray} maximize. \quad L_p(a_1, a_2) &=& \displaystyle \sum_{i=1}^{2} a_i - \frac{1}{2} \sum_{i=1}^{2} a_1 y_1 \left( \sum_{j=1}^{N} a_j y_j K(\boldsymbol{x_i, x_j}) \right) \\ &=& a_1 + a_2 - \frac{1}{2} a_1^2 K(\boldsymbol{x_1, x_1}) - \frac{1}{2} a_2^2 K(\boldsymbol{x_2, x_2}) - a_1 a_2 y_1 y_2 K(\boldsymbol{x_1, x_2}) \\ &&- a_1 y_1 \left( \sum_{j=3}^{N} a_j y_j K(\boldsymbol{x_1, x_j}) \right) - a_2 y_2 \left( \sum_{j=3}^{N} a_j y_j K(\boldsymbol{x_2, x_j}) \right) \end{eqnarray}$
簡略化のため以下とすれば
$\displaystyle K_{i j} \equiv K(\boldsymbol{x_i, x_j}), \quad v_i \equiv \sum_{j=3}^{N} a_j y_j K(\boldsymbol{x_i, x_j}), \quad s_{ij}=y_i y_j $
$maximize. \quad L_p(a_1, a_2) = a_1 + a_2 - \frac{1}{2} a_1^2 K_{11} - \frac{1}{2} a_2^2 K_{22} - a_1 a_2 s_{12} K_{12} - a_1 y_1 v_1 - a_2 y_2 v_2 $
$subject \ to. \quad 0 \leq a_1, a_2 \leq C, \ a_1 y_1 + a_2 y_2 = k $

逐次最小問題最適化法はKKT条件に反する$a_1$が見つかったとき、部分問題の目的関数を最大化するように$a_2$を最適化し、制約条件を満たすように$a_1$を更新する
KKT条件に反する$a_i$がなくなるまで更新を行う

逐次最小問題最適化法におけるKKT条件は以下のものであり、これに反する$a_1$を選ぶ
$\begin{eqnarray} && if[a_i = 0] &&\quad y_i(f_i+h) - 1 \geq 0 \\ && if[0< a_i < C] && \quad y_i(f_i+h) - 1 = 0 \\ && if[a_i = C] && \quad y_i(f_i+h) - 1 \leq 0 \end{eqnarray}$
ここで$f_i \equiv -y_i + \displaystyle \sum_{j=1}^{N} a_j y_j K_{i j} $である

つぎに$a_2$を更新する
$a_2^{new} = a_2^{old} + y_2 \frac{f_1 - f_2}{K_{11}+K_{22} - 2 K_{12}} $

導出は以下になる
$a_1 y_1 + a_2 y_2 = k $の両辺に$y_1$をかけ$a_1$に関する式にして$L_p(a_1, a_2)$から$a_1$を消去
$a_1 = y_1 k - s_{12} a_2$
$L_p(a_2)= (y_1 k - s_{12} a_2) + a_2 + \frac{1}{2}(y_1 k - s_12 a_2)^2 K_{11} - \frac{1}{2}a_s^2 K_{22} - (y_1 k - s_12 a_2)a_2 s_12 K_{12} - (y_1 k - s_12 a_2) y_1 v_1 - a_2 y_2 v_2 $
$L_p(a_2)$が$a_2$について最大値を取るときは偏微分して0になるときなので
$\frac{\partial L_p(a_2)}{\partial a_2} = 1 - s_{12} + s_{12} y_1 k (K_{11}-K_{12}) + s_{12} v_1 y_1 - v_2 y_2 - a_2(K_{11} + 2 K_{12} - K_{22})=0 $
上式を$a_2$について解き$s_{12}, k$を元にもどし$a_2$の更新式となる。
$ \begin{eqnarray} a_2^{new} &=& \frac{1 - s_{12} + s_{12} y_1 k (K_{11} - K_{12}) + s_{12} v_1 y_1 - v_2 y_2 }{K_{11}+K_{22}-2 K_{12}} \\ &=& a_2^{old} + y_2 \frac{f_1-f_2}{K_{11}+K_{22}-2 K_{12}} \end{eqnarray} $

$a_1$の更新後の値が$0 \leq a_1 \leq C$となるよう$a_2$クリッピングをクリッピングする
$if[y_1=y_2] \quad a_2^{new} \in [max(0, a_1^{old}+a_2^{old}-C), min(C, a_1^{old}+a_2^{old})]$
$if[y_1 \neq y_2] \quad a_2^{new} \in [max(0, -a_1^{old}+a_2^{old}), min(C, C-a_1^{old} + a_2^{old})]$

$a_1$を更新する
$a_1^{new} = a_1^{old} - y_1 y_2 (a_2^{new}-a_2^{old})$

関連項目

クラスタリング手法インタフェースクラス
サポートベクタマシン実装編

引用文献

[1] “Pattern Recognition Using Generalized Portrait Method”, Automation and Remote Control, Vladimir N. Vapnik, Aleksandr Lerner, vol.24, pp.774-780, 1963
[2] “Sequential Minimal Optimization: A Fast Algorithm for Training Support Vector Machines”, John C. Platt, Technical Report, MSR-TR-98-14, April, 1998